문제 출처- https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형 | 프로그래머스
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상
programmers.co.kr
-문제-
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.제한사항
- W, H : 1억 이하의 자연수
입출력 예
| W | H | RESULT |
| 8 | 12 |
80 |
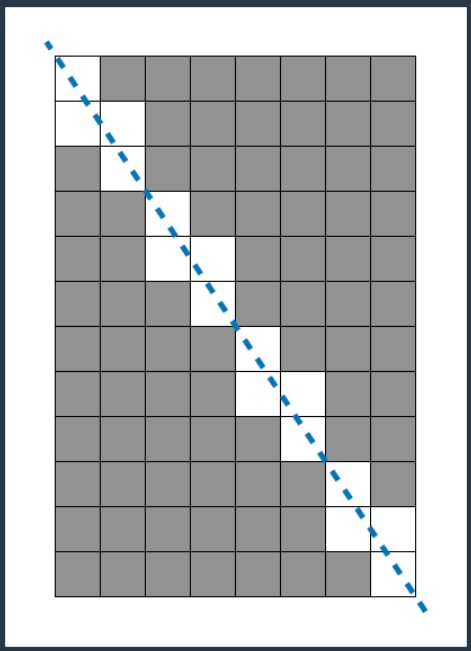
-접근-
1. 처음 시도한 코드는 x축의 width에서 시작하여 0까지 한칸씩 선에 속하는 칸의 개수를 찾아서 전체에서 빼주려고했다. 칸의 개수를 구하는 식은 ceil(y)-floor(prev)이었는데, y는 현재 x에따른 y의 값이고 perv는 x+1에 따른 y값의 값이다.
이 논리에는 문제가 없었는데, double은 오차가 1e-6 ~ 1e-9 정도 있다고 합니다. 이 오차값에 의해서 테스트케이스 6이 통과하지 않았습니다.
2. 1번의 방법대로 해결할 수 없는 이유로 최대 공약수를 이용한 풀이법을 사용하였는데, 선을그어 보면 y값이 소수값을 가지지않고 정수값을 가지는 경우를 나눠서 보면 일정 블록크기를 가진 패턴이 있다는걸 알 수 있는데,
해당 블록의 x길이는 width를 height와width의 최대공약수로 나눈 길이고, y길이는 height와width의 최대공약수로 나눈 길이입니다.
해당 블록에서 선이 지나가는 칸의 갯수는 x길이+y의길이 -1임을 이용해서 선이 지나가는 전체 칸수를 모두 구하여줬습니다.
-코드-
1번 접근(6번 케이스 오답)
#include <iostream>
#include <math.h>
using namespace std;
long long solution(int w, int h)
{
long long answer = 0;
long long minus = 0;
// 직선의 방정식을 구해서
// x범위에 따른 y 시작 y끝의 개수세자.
double y;
double lean = -double(h) /double(w);
double prev = 0;
for (int i = w; i >= 0; i--) {
y = lean * double(i)+ double(h);
long cnt = long(ceil(y)) - long(floor(prev));
prev = y;
minus +=cnt;
}
answer = long(h) *long(w) - long(minus);
return answer;
}
2번 접근(정답)
#include <iostream>
using namespace std;
long long solution(int w, int h)
{
int gcd;
long long sum = (long long)w * (long long)h;
int start = w<h ? w: h;
for (int i = start; i > 0; i--) { //최대 공약수 구하기
if ((w % i == 0) && (h % i == 0)) {
gcd = i;
break;
}
}
return sum - gcd * ((w / gcd) + (h / gcd) - 1);
}
혹시 1번 코드를 수정하여 정답이 나올 수 있는 방법이 있다면 공유부탁드립니다 ㅠㅠ
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 - 거스름돈(Level 3)/Wanna Be 컴잘알 (0) | 2019.12.10 |
|---|---|
| 프로그래머스 - 보행자천국(Level 3)/Wanna Be 컴잘알 (0) | 2019.12.10 |
| 프로그래머스 - 가장 긴 팰린드롬(Level 3)/Wanna Be 컴잘알 (0) | 2019.11.27 |
| 프로그래머스 - 저울(Level 3)/Wanna Be 컴잘알 (0) | 2019.11.27 |
| 프로그래머스 - 입국심사(Level 3)/Wanna Be 컴잘알 (1) | 2019.11.22 |

